Skip to content

Uniswap V3

Created at: Updated at: v1 · 735
DeFi, DEX

Uniswap V2 采用 CFMM 恒定函数做市商算法，池子的流动性是分布在无穷区域上的，池子允许在任何价格的交易发生，从 0 到正无穷。但一个资产的历史价格通常是在某个区间内的，不管这个区间是大还是小，在远离当前价格区间的、永远不会达到的某个点上提供流动性是毫无意义的。

Uniswap V3 引入了 集中流动性(concentrated liquidity) 的概念：LP 可以选择他们希望在哪个价格区间提供流动性。这个机制通过将更多的流动性提供在一个相对狭窄的价格区间，大大提高了资产利用效率。

Uniswap V3 的 tick 之间的工作机制跟 V2 完全一样，tick 之间的流动性是可以完全耗尽的。

下面了解几个公式：

  • L = \sqrt{xy} 池子中的流动性是两种 token 资产数量的组合。两种代币数量乘积为 k，因此我们可以用 \sqrt{xy} 来衡量池子流动性。L 实际上是 x 和 y 的几何平均数。
  • \sqrt{P}= \sqrt{\frac{x}{y}} 这里 \frac{x}y 是 token0 相对于 token1 的价格。
  • 输出数量 ∆y 在交易中满足 L=\frac{∆y}{∆\sqrt{P}}，这里 ∆y 是交易中 token y 变化的数量，∆\sqrt{P} 是交易中 \sqrt{P} 变化的数量。这个公式成立的根本是交易行为不能导致 L 发生变化，\sqrt{xy} = \sqrt{x_0 y_0} = \sqrt{x_1 y_1} 交易前后 L 不变，详见 Uniswap V3 Book。
  • 因为双方的价格互为倒数，所以 输入数量 ∆x = ∆\frac{1}{\sqrt{P}}L

Ticks

Price ranges and ticks

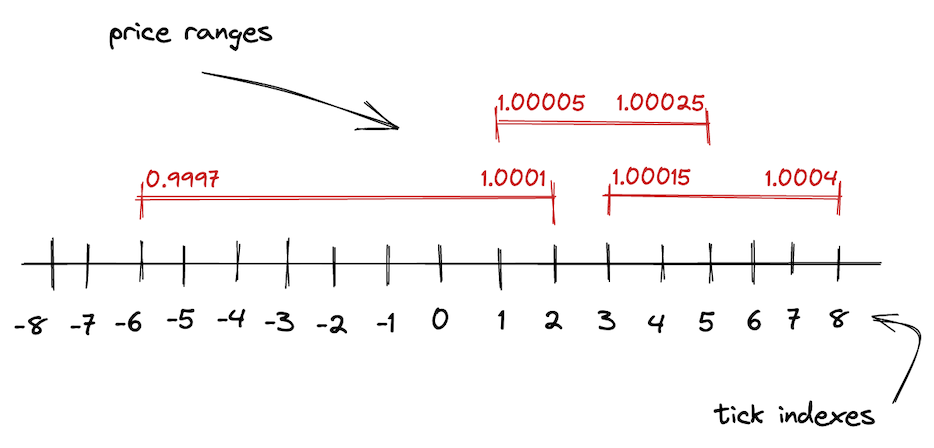
Ticks 是 V3 中的一大核心，V2 中的无穷价格区间在 V3 中被分成了更小的价格区间，每个区间都由上下界端点进行限制。为了进行这些边界的协调，V3 引入了 ticks。价格不能落在两个相邻的 tick 之间，只能落到 tick 上。

每个 tick 有一个 index 和对应的价格：p(i) = 1.0001^i，p(i) 即为 tick i 的价格。但因为 Uniswap V3 储存的是 \sqrt{P} 而不是 P，所以这个公式实际是 \sqrt{p(i)}=\sqrt{1.0001^i} = 1.0001^{\frac{i}{2}}，所以他的值大概是 \sqrt{p(0)}=1，\sqrt{p(1)}≈1.00005，\sqrt{p(-1)}≈0.99995。

在 V3 中 \sqrt{P} 使用 Q64.96 储存，受限于数据长度，能够保存的价格范围是 [-2^{2*64},2^{2*64}]，所以对应的 ticks 的取值范围为 [log_{1.0001}2^{-128},log_{1.0001}2^{128}] = [−887272, 887272]。

计算流动性

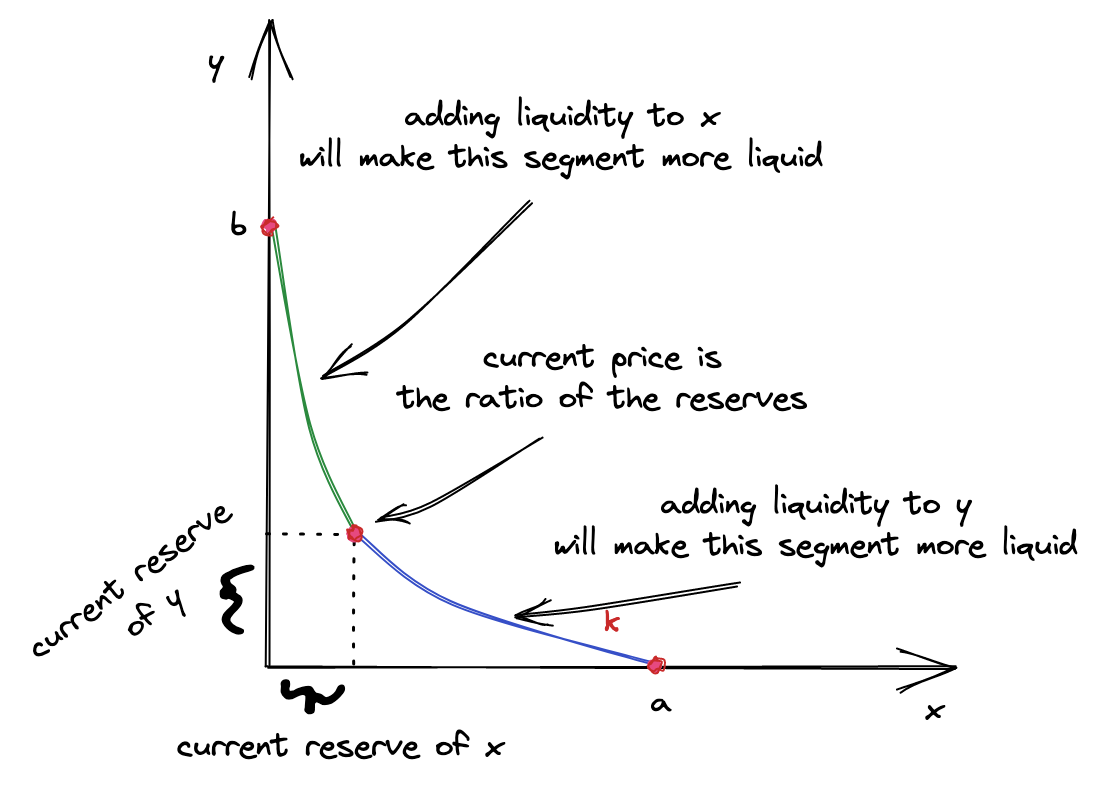
Liquidity on the curve

Liquidity 计算

根据之前的公式 结合上图计算流动性 L 的值，

将公式 ∆x=∆\frac{1}{\sqrt{P}}L 展开一下 ∆x=(\frac{1}{\sqrt{P_c}} - \frac{1}{\sqrt{P_b}})L 则 L=∆x\frac{\sqrt{P_b}\sqrt{P_c}}{\sqrt{P_b}-\sqrt{P_c}}

将公式 ∆y=(\sqrt{P_c} - \sqrt{P_a})L 则 L=\frac{∆y}{\sqrt{P_c}-\sqrt{P_a}}

重新计算 token 数量

因为我们使用 ∆x 和 ∆y 计算出了两个不同的 L，我们会用小的那个。所以最初用来计算的 ∆x 和 ∆y 需要代入上一步的公式中使用小的 L 重新计算 ∆x 和 ∆y 这是最终用户会添加进去的流动性。

Swap 计算

比如我们要实现一个 Uniswap V3 like 的 DEX 的聚合器，Swap 的 input / output amount 的计算是绕不过去的，最简单的思路就是通过 RPC 调用 Quote 合约查询 output amount，但是这里有一个弊端就是通过 Quote 合约查询的结果是跨多个 tick 执行完成后的最终结果。这种情况下我们没法知道 pool 的每个 tick 的流动性，比如想要将 10000 A 换成 B，pool 中在价格

  • tick1: 100 A = 1 B 处有 10 B 流动性
  • tick2: 150 A = 1 B 处有 10 B 流动性
  • tick3: 200 A = 1 B 处有 40 B 流动性

所以 tick1 用 1000A 换了 10B 还 9000A，然后 tick2 1500A 换了 10B 还 7500A，tick3 7500A 换了 37.5B 兑换完成，quote 合约返回了一个 57.5B 的结果。设想一下如果还有一个路径是 A->C->B，它的计算后价格是 110 A = 1 B 这个价格下的流动性有 40 B，你如何在不知道每个 tick 下流动性的情况下严谨的拆分订单？

所以要想知道每个 tick 下的流动性，有两种方法，

  1. 部署一个修改版 Quote 合约，把每个 tick 上的流动性也返回回来。
  2. 拿到一些基础的数据，比如 slot0 中的当前价格、流动性，即当前价格的 position 对应的当前及上下一位 wordPos 的 bitmap 数据，即对应已初始化 tick 的 TickInfo，通过其他语言在链下实现相同的逻辑，也可以准确的计算出 output amount。

奶爸为你趟了一遍坑，结论是可行的，通过用 go 重新实现了 tick、tick math、liquidity math、full math、bitmap 合约中的一些方法，奶爸成功在链下仅用几个链上数据实现了 exactInput 的 output amount 的计算。

inputToken := common.HexToAddress("0xA0b86991c6218b36c1d19D4a2e9Eb0cE3606eB48")
outputToken := common.HexToAddress("0x853d955aCEf822Db058eb8505911ED77F175b99e")
amountIn := big.NewInt(19000000000000)

token0, token1 := sortToken(&inputToken, &outputToken)
println("token0", token0.String())
println("token1", token1.String())

isZerForOne := token0 == &inputToken
println("isZerForOne", isZerForOne)

client, err := ethclient.Dial("https://cloudflare-eth.com")
if err != nil {
	panic(err)
}
pool, err := contracts.NewUniswapV3Pool(common.HexToAddress("0xc63b0708e2f7e69cb8a1df0e1389a98c35a76d52"), client)
if err != nil {
	panic(err)
}

fee, err := pool.Fee(nil)
if err != nil {
	panic(err)
}

token0FromPool, err := pool.Token0(nil)
if err != nil {
	panic(err)
}
token1FromPool, err := pool.Token1(nil)
if err != nil {
	panic(err)
}

if token0FromPool != *token0 || token1FromPool != *token1 {
	panic("token0 or token1 is not match")
}

callOpts := &bind.CallOpts{
	BlockNumber: big.NewInt(19760163),
}

liquidity, err := pool.Liquidity(callOpts)
if err != nil {
	panic(err)
}

tickSpacing, err := pool.TickSpacing(callOpts)
if err != nil {
	panic(err)
}

slot0, err := pool.Slot0(callOpts)
if err != nil {
	panic(err)
}

quoterV2, err := contracts.NewUniswapV3QuoterV2(common.HexToAddress("0x61fFE014bA17989E743c5F6cB21bF9697530B21e"), client)
if err != nil {
	panic(err)
}

sqrtPriceMin, err := v3utils.GetSqrtRatioAtTick(v3utils.MaxTick - 1)
if err != nil {
	panic(err)
}

ret, err := quoterV2.QuoteExactInputSingle(callOpts, contracts.IQuoterV2QuoteExactInputSingleParams{
	TokenIn:           inputToken,
	TokenOut:          outputToken,
	AmountIn:          amountIn,
	Fee:               fee,
	SqrtPriceLimitX96: sqrtPriceMin,
})
if err != nil {
	panic(err)
}
fmt.Printf("on-chain ret: %+v\n", ret)

var state SwapState
state.AmountSpecifiedRemaining = new(big.Int).Set(amountIn)
state.SqrtPriceX96 = slot0.SqrtPriceX96
state.Liquidity = liquidity
state.Tick = slot0.Tick
state.AmountCalculated = big.NewInt(0)

for !lib.IsZero(state.AmountSpecifiedRemaining) && lib.Ne(state.SqrtPriceX96, sqrtPriceMin) == 1 {

	fmt.Printf("\n\n\n======== amountRemaining: %d =========\n", state.AmountSpecifiedRemaining.Int64())

	var step StepComputations
	step.SqrtRatioStartX96 = state.SqrtPriceX96

	tickmapKey := lib.GetTickMapKeyForTick(int(slot0.Tick.Int64()), int(tickSpacing.Int64()), isZerForOne)
	tickMap := make(map[int]*big.Int)
	for i := int(tickmapKey) - 1; i <= int(tickmapKey)+1; i++ {
		v, err := pool.TickBitmap(callOpts, int16(i))
		if err != nil {
			panic(err)
		}
		tickMap[i] = v
	}
	fmt.Printf("tickMap: %+v\n", tickMap)

	step.Initilized, step.TickNext = lib.NextInitializedTickWithinOneWord(tickMap, int(state.Tick.Int64()), int(tickSpacing.Int64()), isZerForOne)
	fmt.Printf("nextTickInitialized: %t, nextTick: %d\n", step.Initilized, step.TickNext)

	if step.TickNext < v3utils.MinTick {
		step.TickNext = v3utils.MinTick
	} else if step.TickNext > v3utils.MaxTick {
		step.TickNext = v3utils.MaxTick
	}

	step.SqrtPriceNextX96, err = lib.GetSqrtRatioAtTick(step.TickNext)
	if err != nil {
		panic(err)
	}

	var sqrtRatioTargetX96 *big.Int
	var flag bool
	if isZerForOne {
		flag = lib.Gt(step.SqrtPriceNextX96, state.SqrtPriceX96) == 1
	} else {
		flag = lib.Gt(step.SqrtPriceNextX96, sqrtPriceMin) == 1
	}
	if flag {
		sqrtRatioTargetX96 = sqrtPriceMin
	} else {
		sqrtRatioTargetX96 = step.SqrtPriceNextX96
	}

	state.SqrtPriceX96, step.AmountIn, step.AmountOut, step.FeeAmount, err = v3utils.ComputeSwapStep(state.SqrtPriceX96, sqrtRatioTargetX96, state.Liquidity, state.AmountSpecifiedRemaining, constants.FeeAmount(fee.Uint64()))
	if err != nil {
		panic(err)
	}
	fmt.Printf("sqrtRatioNext: %s, retAmtIn: %s, amtOut: %s, feeAmt: %s\n", state.SqrtPriceX96.String(), step.AmountIn.String(), step.AmountOut.String(), step.FeeAmount.String())
	fmt.Printf("state: %+v\n", state)

	// if exactInput {
	state.AmountSpecifiedRemaining.Sub(state.AmountSpecifiedRemaining, new(big.Int).Add(step.AmountIn, step.FeeAmount))
	state.AmountCalculated.Sub(state.AmountCalculated, step.AmountOut)
	// } else {
	//    TODO: exactOutput
	// }

	if lib.Ne(state.SqrtPriceX96, step.SqrtPriceNextX96) == 0 {
		if step.Initilized {
			tickInfo, err := pool.Ticks(callOpts, big.NewInt(int64(step.TickNext)))
			if err != nil {
				panic(err)
			}
			liquidityNet := tickInfo.LiquidityNet
			if isZerForOne {
				liquidityNet.Neg(liquidityNet)
			}
			state.Liquidity = lib.AddDelta(state.Liquidity, liquidityNet)
		}
		if isZerForOne {
			state.Tick.SetInt64(int64(step.TickNext) - 1)
		} else {
			state.Tick.SetInt64(int64(step.TickNext))
		}
	} else if lib.Ne(state.SqrtPriceX96, step.SqrtPriceNextX96) == 1 {
		tick, err := lib.GetTickAtSqrtRatio(state.SqrtPriceX96)
		if err != nil {
			panic(err)
		}
		state.Tick.SetInt64(int64(tick))
	}

}

var amount0, amount1 *big.Int
// if isZerForOne == exactInput {
amount0 = new(big.Int).Sub(amountIn, state.AmountSpecifiedRemaining)
amount1 = new(big.Int).Set(state.AmountCalculated)
// } else {
//    TODO: exactOutput
// }

fmt.Printf("\n\n\nisZeroForOne: %t, amountIn: %d, state: %+v\n", isZerForOne, amountIn, state)
fmt.Printf("amount0: %s, amount1: %s\n", amount0.String(), amount1.String())

if amount1.CmpAbs(ret.AmountOut) != 0 {
	panic("amount1 is not match")
}

核心就在 Pool 合约中的 swap 方法，一步一步实现即可，下面是执行后的效果。

token0 0x853d955aCEf822Db058eb8505911ED77F175b99e
token1 0xA0b86991c6218b36c1d19D4a2e9Eb0cE3606eB48
isZerForOne false
on-chain ret: {AmountOut:+18996651967770371746104874 SqrtPriceX96After:+79262835938196828630617 InitializedTicksCrossed:3 GasEstimate:+144147}



======== amountRemaining: 19000000000000 =========
2024/05/06 22:47:47 tick = -276340, tickSpacing = 10, zeroForOne = false
2024/05/06 22:47:47 compressed = -27634
tickMap: map[-109:+25711008708143844408671393477458601640355247900524685364822016 -108:+633825300114114700748472448192 -107:+0]
nextTickInitialized: true, nextTick: -276330
sqrtRatioNext: 79204503519858955838074, retAmtIn: 7327321285028, amtOut: 7335092912385649064434176, feeAmt: 3665493390
state: {AmountSpecifiedRemaining:+19000000000000 AmountCalculated:+0 SqrtPriceX96:+79204503519858955838074 Liquidity:+15842738790231437704582 Tick:-276340}



======== amountRemaining: 11669013221582 =========
2024/05/06 22:47:51 tick = -276330, tickSpacing = 10, zeroForOne = false
2024/05/06 22:47:51 compressed = -27633
tickMap: map[-109:+25711008708143844408671393477458601640355247900524685364822016 -108:+633825300114114700748472448192 -107:+0]
nextTickInitialized: true, nextTick: -276320
sqrtRatioNext: 79244113692861321940131, retAmtIn: 7919825073883, amtOut: 7920596115673192183308463, feeAmt: 3961893484
state: {AmountSpecifiedRemaining:+11669013221582 AmountCalculated:-7335092912385649064434176 SqrtPriceX96:+79244113692861321940131 Liquidity:+15841213013653411008977 Tick:-276330}



======== amountRemaining: 3745226254215 =========
2024/05/06 22:47:53 tick = -276320, tickSpacing = 10, zeroForOne = false
2024/05/06 22:47:53 compressed = -27632
tickMap: map[-109:+25711008708143844408671393477458601640355247900524685364822016 -108:+633825300114114700748472448192 -107:+0]
nextTickInitialized: true, nextTick: -276310
sqrtRatioNext: 79262835938196828630617, retAmtIn: 3743353641087, amtOut: 3740962939711530498362235, feeAmt: 1872613128
state: {AmountSpecifiedRemaining:+3745226254215 AmountCalculated:-15255689028058841247742639 SqrtPriceX96:+79262835938196828630617 Liquidity:+15840996916216165493682 Tick:-276320}



isZeroForOne: false, amountIn: 19000000000000, state: {AmountSpecifiedRemaining:+0 AmountCalculated:-18996651967770371746104874 SqrtPriceX96:+79262835938196828630617 Liquidity:+15840996916216165493682 Tick:-276316}
amount0: 19000000000000, amount1: -18996651967770371746104874

结果是当我们知道了 pool 中每个 tick 的流动性，我们可以合理的将订单拆分。

  • 4400 A -> C -> 40 B
  • 4600 A -> 37.5 B

最终我们通过合理拆分订单可以多得到 20 B，当然实际的情况比这个要复杂，本文旨在探索 off-chain 计算的可行性。

Comments

Commenting as a guest. A nickname is required; email is optional. Only new comments posted after verifying your email and signing in will appear on your profile. Existing guest comments will not be linked automatically.

Register

Share article

Uniswap V3

Email X

View original ↗