Shamir's Secret Sharing 秘密分享

·v1 | 👀493
Crypto

作者 Shamir 是 RSA 命名中的 S。

如果你看不懂公式，可以跟着展开的简化公式一点一点跟着算来理解。本文是不安全的 Shamir's Secret Sharing 的简单例子，不能直接使用，

假设你有一些资产存放在保险库，这个保险库有设置一个密码，你想交给 n 个人保管，至少凑齐其中 t 个人才能打开保险库。

split

  1. 确定阈值，6 份密钥，至少 4 份密钥才能打开保险库，n = 6, t = 4

  2. 秘密的选择打开保险库的正确密码 K，如 K=13

  3. 秘密的选择 t-1 个随机数，如 a_1 = 8, a_2 = 19, a_3 = 11 （生成 t-1 个随机数的原因是解方程组要满足 多项式数量 >= 未知数个数，达到了门限签名的目的）

  4. 分别计算 P(x) = K + \sum\limits_{j=1}^{t-1}a_jx^j，6 份密钥计算分别展开 P(x) = K + a_1\cdot x^1 + a_2\cdot x^2 + a_3\cdot x^3 如下：
    P(1) = 13 + (8 \cdot 1^1) + (19 \cdot 1^2) + (11 \cdot 1^3) = 13 + 8 + 19 + 11 = 51

    P(2) = 13 + (8 \cdot 2^1) + (19 \cdot 2^2) + (11 \cdot 2^3) = 13 + 16 + 76 + 88 = 193

    P(3) = 13 + (8 \cdot 3^1) + (19 \cdot 3^2) + (11 \cdot 3^3) = 13 + 24 + 171 + 297 = 505

    P(4) = 13 + (8 \cdot 4^1) + (19 \cdot 4^2) + (11 \cdot 4^3) = 13 + 32 + 304 + 704 = 1053

    P(5) = 13 + (8 \cdot 5^1) + (19 \cdot 5^2) + (11 \cdot 5^3) = 13 + 40 + 475 + 1375 = 1903

    P(6) = 13 + (8 \cdot 6^1) + (19 \cdot 6^2) + (11 \cdot 6^3) = 13 + 48 + 684 + 2376 = 3121

  5. 将 P(i) 作为密钥交给第 i 个人，不要被其他人看到

recover

只要知道 4 个人的密钥和他们在所有人中的位置，即可还原出原始秘密 K。

  1. 假设集齐了 P(2), p(3), P(5), P(6)

  2. 接下来就是方程组求解了，我们知道 P(2), p(3), P(5), P(6)，求 K 和 a_j，方程组：
    K+ a_1\cdot 2^1 + a_2\cdot 2^2 + a_3\cdot 2^3 = 193

    K+ a_1\cdot 3^1 + a_2\cdot 3^2 + a_3\cdot 3^3 = 505

    K+ a_1\cdot 5^1 + a_2\cdot 5^2 + a_3\cdot 5^3 = 1903

    K+ a_1\cdot 6^1 + a_2\cdot 6^2 + a_3\cdot 6^3 = 3121

  3. 使用 四元一次方程组计算器 最终可解得：K=13, a_1 = 8, a_2 = 19, a_3 = 11

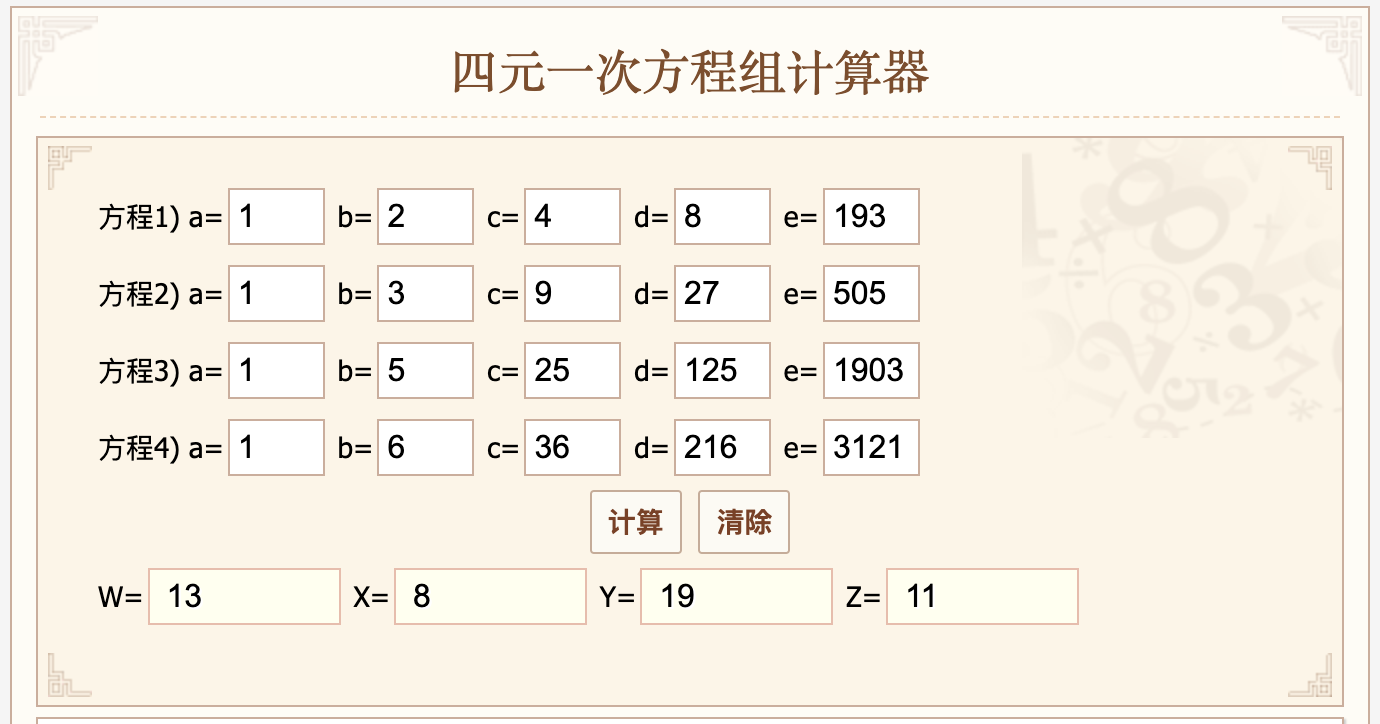
image.png

实际的要复杂一些，后面可能会去搞懂，毕竟这篇文章也是写在实际应用一年之后了。念念不忘，必有回响。

Comments